Présentation du projet #
J’ai réalisé ce projet à la fin du premier semestre de ma première année d’école d’ingénieur, l’objectif était de mobiliser nos connaissances en mathématiques appliquées et en particulier en probabilités et statistiques sur un cas concret. Nous étions 4 pour effectuer ce projet qui a duré 2 semaines.
Le sujet de ce projet était l’analyse statistique de données de dégradation. En effet, pour certains systèmes, connaître la date d’une future défaillance pour anticiper la maintenance peut être d’une importance capitale. Cela peut être justifié par un coût de remplacement élevé ou par les conséquences graves qu’entraînerait une défaillance, on peut citer par exemple le cas de l’effondrement du pont de Gênes en 2018 en Italie. L’objectif final est donc de modéliser le niveau de dégradation d’un système à partir de données récoltées, puis de prédire la date du franchissement d’un seuil critique fixé.
Méthodologie #
Pour modéliser le niveau de défaillance des systèmes, l’outil qui vient naturellement est l’utilisation de processus stochastiques. Un processus stochastique est l’évolution d’un phénomène au fil du temps dont le parcours dépend, en partie, du hasard. Lors de notre projet, nous avons utilisé deux types de processus : le processus Gamma et le processus de Wiener. Le processus Gamma modélise une évolution strictement croissante (ses incréments sont de loi Gamma). Le processus de Wiener, quant à lui, modélise un niveau qui peut diminuer ou croître (ses incréments sont de loi normale), c’est un processus très connu en finance et en physique car il permet de modéliser le mouvement brownien. Nous avons considéré ces deux processus sous leur forme homogène, c’est-à-dire à accroissements stationnaires (la loi des accroissements ne change pas au fil du temps). Ils sont définis par des paramètres réels contrôlant la dérive et la diffusion pour le processus de Wiener, et la forme et le taux pour le processus Gamma.
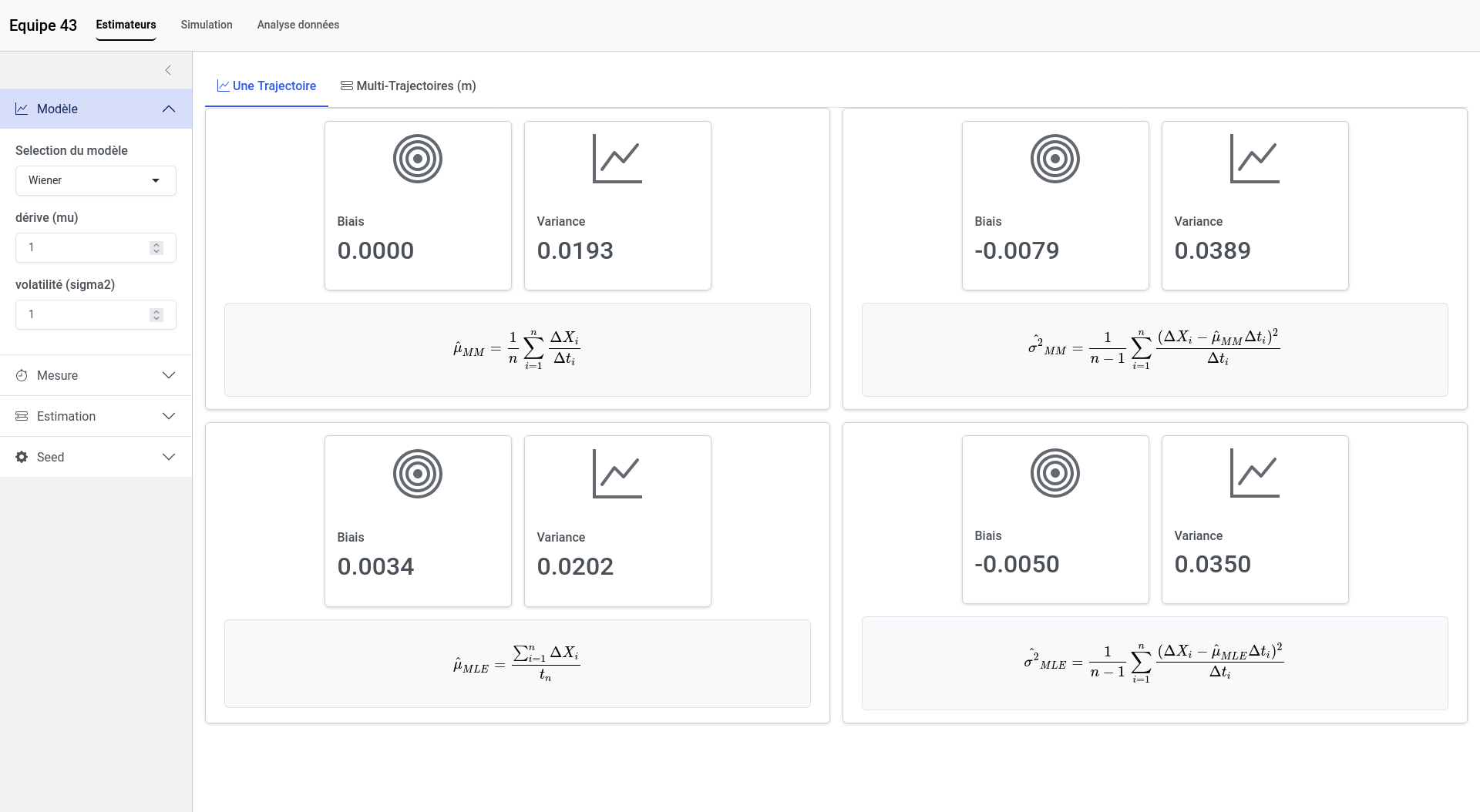
C’est donc ces paramètres qu’il va falloir estimer pour modéliser la défaillance à partir des données. Notre première tâche importante a donc été la mise au point d’estimateurs qui permettent de déterminer la valeur des paramètres à partir des observations empiriques. Il nous tenait à cœur de faire ce travail par nous-mêmes pour bien comprendre les méthodes utilisées, dans notre cas la méthode des moments et du maximum de vraisemblance, mais nous nous sommes aussi appuyés sur certains ouvrages12. Pour chacun des estimateurs que nous avions trouvés, il était nécessaire de contrôler sa qualité (biais et variance), pour cela nous avons utilisé des méthodes empiriques avec des simulations que nous avons programmées en langage R.
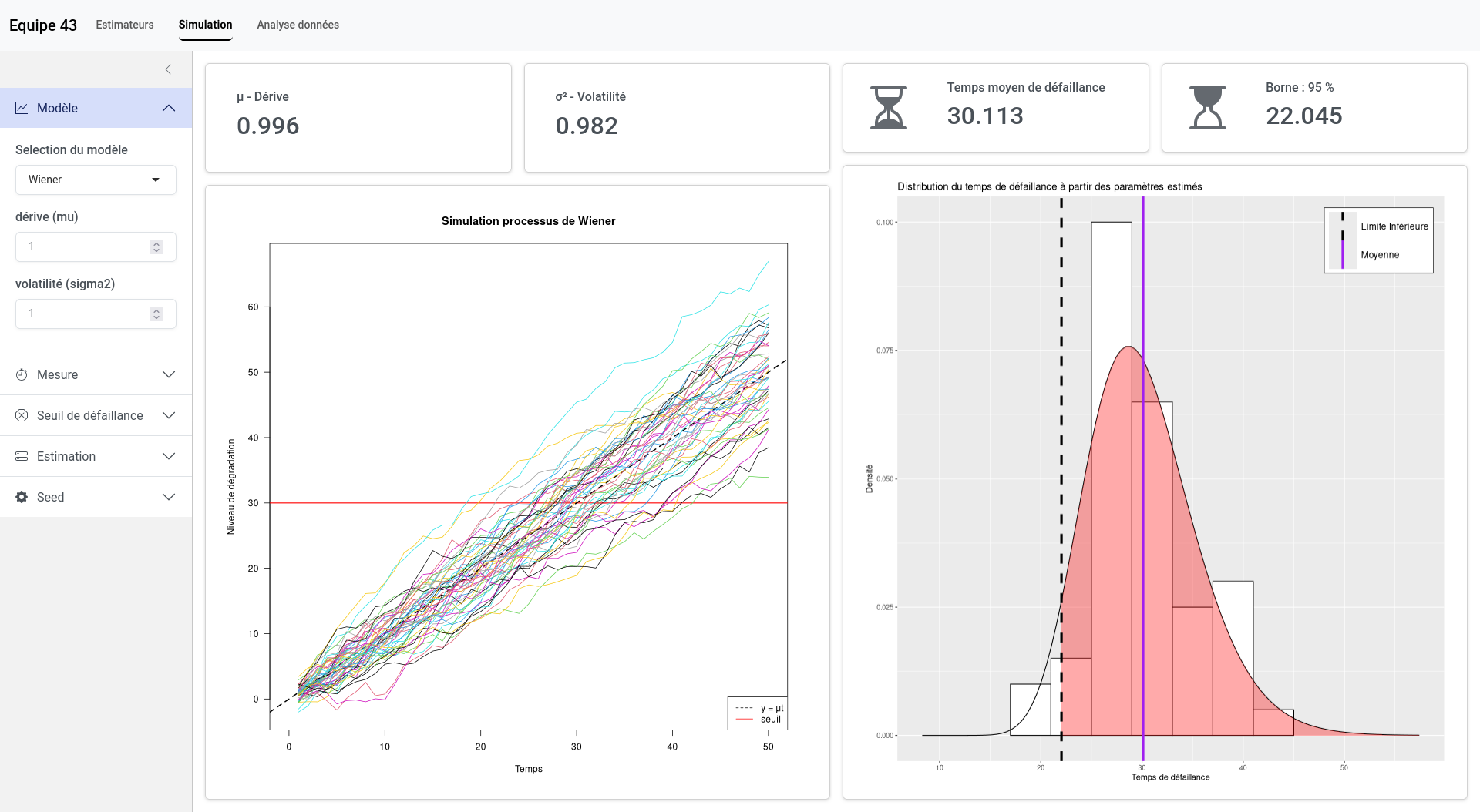
Une fois que nous étions capables de modéliser les processus de dégradation, il était nécessaire de prédire le temps de défaillance. En effet, le temps du franchissement du seuil suit une certaine loi de probabilité, par exemple, dans le cas d’un processus de Wiener, c’est une loi inverse-gaussienne. À partir de cette loi, nous pouvions calculer le temps moyen de défaillance, mais aussi la borne inférieure qui donnait une date telle que 95% des défaillances soient après cette date, ce qui peut être utile dans le cas de maintenances préventives.
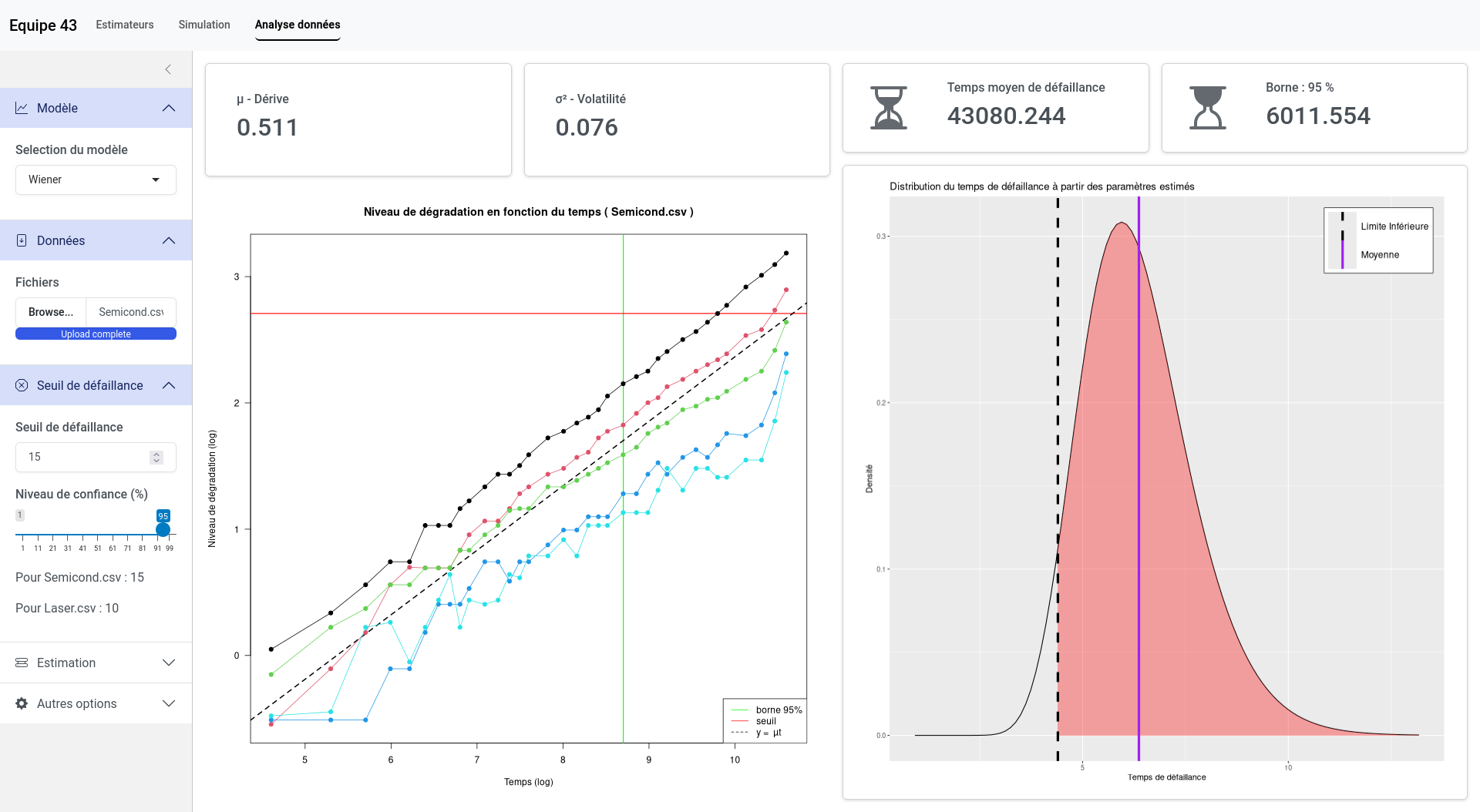
Finalement, la dernière étape de notre travail consistait à analyser deux jeux de données qui nous étaient fournis. Le premier concernait la dégradation par porteurs chauds des semi-conducteurs qui est une usure progressive due à l’impact répété de porteurs de charge très énergétiques à l’intérieur du transistor. Le second portait sur des lasers, l’indicateur de dégradation était le courant de fonctionnement requis pour maintenir une sortie lumineuse constante. Nous avons donc appliqué nos modèles sur ces données, cependant, quelques adaptations ont été nécessaires pour que les hypothèses des modèles soient validées. Par exemple, avec les semi-conducteurs nous avons utilisé une échelle log-log pour s’assurer que la tendance était linéaire et nous avons effectué une translation des données pour éviter les valeurs négatives.
Résultats #
Durant ces deux semaines, j’ai beaucoup appris les méthodes d’analyse statistiques et les modèles stochastiques. Le projet a été globalement une réussite et nous avons réussi à livrer des résultats pertinents ainsi qu’une bonne maîtrise de la méthodologie de modélisation.
Un autre point très important est qu’il nous était demandé de concevoir une application pour visualiser, simuler et reproduire l’ensemble des étapes de la modélisation. Nous avons donc développé une application web à l’aide de la bibliothèque Shiny en R. Les fonctionnalités de celle-ci sont les suivantes :
- simulation de processus de Wiener et Gamma entièrement paramétrable,
- test de la qualité des estimateurs par simulation,
- analyse paramétrable d’un jeu de données.
À la fin de notre projet nous avons pu commencer à explorer des modèles plus complexes avec l’utilisation de processus de Wiener non homogènes, c’est-à-dire que les accroissements ne suivent plus une loi normale \(\mathcal{N}(\mu\Delta t, \sigma^2 \Delta t)\) mais une loi normale \(\mathcal{N}(\mu(\Delta t)^{\alpha}, \sigma^2 \Delta t)\). Nous avons réussi à estimer les paramètres de ce type de processus avec la méthode du maximum de vraisemblance et une régression linéaire. Cependant, nous n’avons pas eu le temps de l’appliquer à nos données. D’autres approfondissements étaient possibles, tel que l’utilisation de processus Gamma non homogènes ou encore la modélisation de processus de Wiener avec maintenance imparfaite.